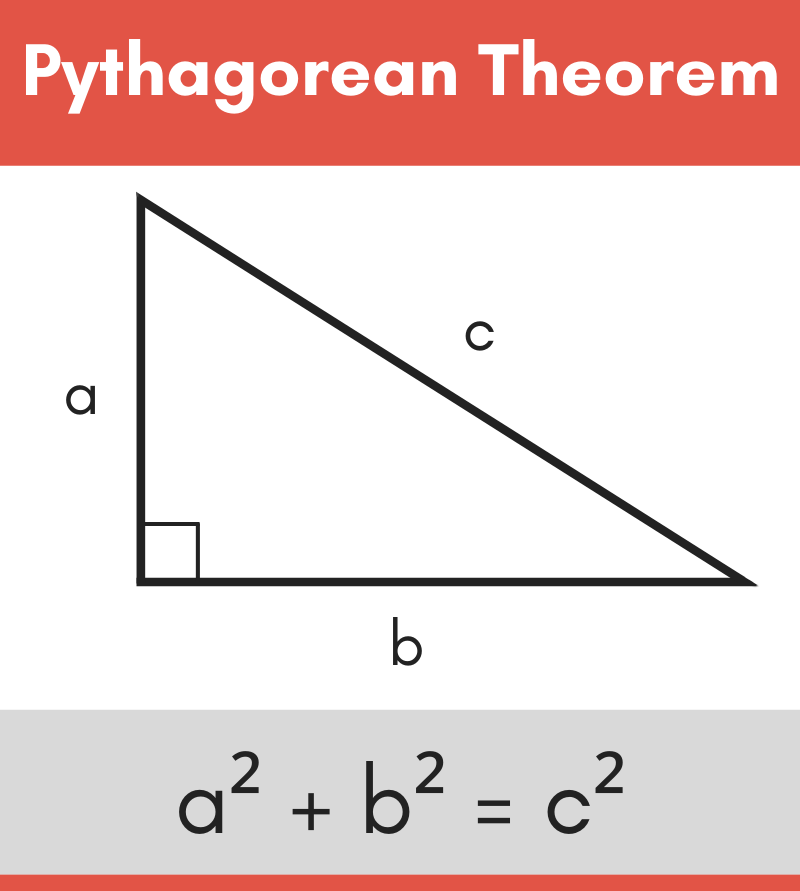
Concept 15 Pythagorean Theorem In mathematics the Pythagorean theorem or Pythagoras theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle It states that the area of the square whose side is the hypotenuse the side opposite the right angle is equal to the sum of the areas of the squares on the other two sides
Pythagoras Theorem also called Pythagorean Theorem is an important topic in Mathematics which explains the relation between the sides of a right angled triangle The sides of the right triangle are also called Pythagorean triples The formula and proof of this theorem are explained here with examples The Pythagorean Theorem guarantees that if we know the lengths of two sides of a right triangle we can always determine the length of the third side Here are the three variations of the Pythagorean Theorem formulas Let s go over some examples Examples of Applying the Pythagorean Theorem Example 1 Find the length of the hypotenuse
Concept 15 Pythagorean Theorem
Concept 15 Pythagorean Theorem
https://content.jwplatform.com/thumbs/B7f0QGPm-1280.jpg
Pythagoras Theorem Explained
https://image1.slideserve.com/3193820/examples-of-the-pythagorean-theorem-l.jpg
Visualizing General Case Of Pythagorean Theorem VIDEO
https://i1.wp.com/tapintoteenminds.com/wp-content/uploads/2014/06/Pythagorean-Theorem-Introduce-the-Algebraic-Formula.png?ssl=1
The core aspect of this theorem is to find the measure of an unknown length or an unknown angle of a right angled triangle The Pythagorean theorem is a cornerstone of math that helps us find the missing side length of a right triangle In a right triangle with sides A B and hypotenuse C the theorem states that A B C The hypotenuse is the longest side opposite the right angle Created by Sal Khan Questions Tips Thanks Want to join the conversation
Pythagorean theorem the well known geometric theorem that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse the side opposite the right angle or in familiar algebraic notation a2 b2 c2 Two Algebraic Proofs using 4 Sets of Triangles The theorem can be proved algebraically using four copies of a right triangle with sides a a b b and c c arranged inside a square with side c c as in the top half of the diagram The triangles are similar with area frac 1 2 ab 21ab while the small square has side b a b a and area
More picture related to Concept 15 Pythagorean Theorem
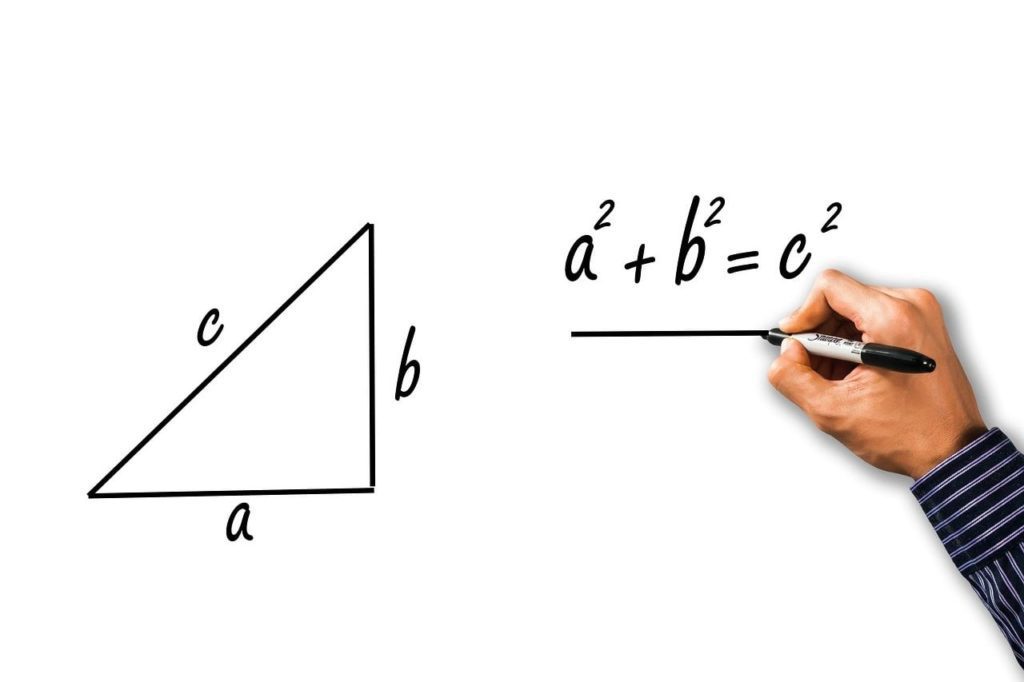
Concept Of Pythagoras Theorem And Why It Is Important General
https://b2962890.smushcdn.com/2962890/wp-content/uploads/Pythagoras-theorem-1024x682.jpg?lossy=1&strip=1&webp=1
Pythagoras Theorem Explained
https://image2.slideserve.com/3660544/pythagorean-theorem-l.jpg
An Introduction To Pythagoras Theorem SyedLearns
https://www.syedlearns.co/wp-content/uploads/2021/04/167768488_218533083355223_5467976182138651161_n.png
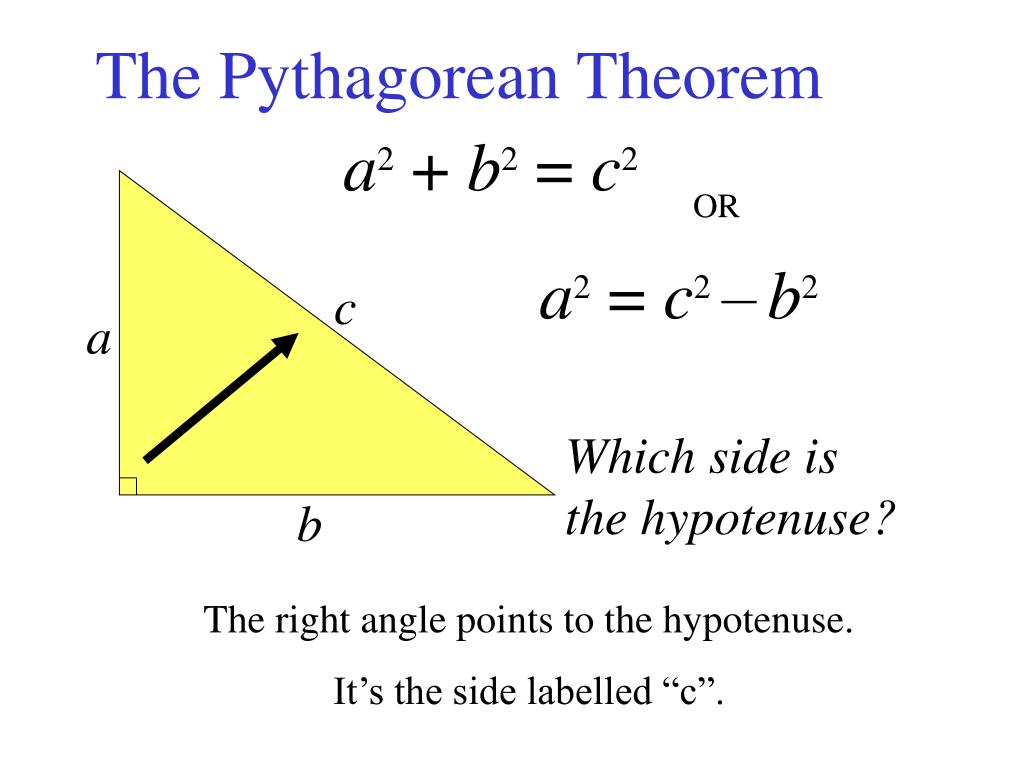
The Pythagorean Theorem If a and b are the lengths of the legs of a right triangle and is the length of the hypotenuse then the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse This relationship is represented by the formula a2 b2 c2 The theorem means that if we know the lengths of any two sides of a right triangle we can find out the length of the last side We can find right triangles all over the place inside of prisms and pyramids on maps when we re finding distance even hiding inside of equilateral triangles Practice Problem 1 1
ThePythagorean theoremis one of the most beautiful theorems in mathematics It is simple to state easy to use and highly accessible it doesn t require a huge amountofmathematical machinery to prove We llbe ableto proveit innumerous ways with what we ve learned so far The Pythagorean theorem states that with a right angled triangle the sum of the squares of the two sides that form the right angle is equal to the square of the third longer side which is called the hypotenuse
PPT The Pythagorean Theorem PowerPoint Presentation Free Download
https://image.slideserve.com/1321254/slide1-l.jpg
How To Prove The Pythagorean Theorem 10 Steps with Pictures
http://www.wikihow.com/images/0/02/Prove-the-Pythagorean-Theorem-Step-10.jpg
Concept 15 Pythagorean Theorem - The Pythagorean Theorem also known as the Pythagoras Theorem is one of the most fundamental theorems in mathematics and it defines the relationship between the three sides of a right angled triangle In a right angled triangle one of the angles is 90 and the side that is opposite to that 90 right angle is known as the hypotenuse The other two sides that are adjacent to the right