Trig Sub Chart Trig substitution is a somewhat confusing technique which despite seeming arbitrary esoteric and complicated at best is pretty useful for solving integrals for which no other technique we ve learned thus far will work Trig substitution list There are three main forms of trig substitution you should know p TS1 If you see a2 x2
In mathematics trigonometric substitution is the replacement of trigonometric functions for other expressions In calculus trigonometric substitution is a technique for evaluating integrals Moreover one may use the trigonometric identities to simplify certain integrals containing radical expressions Like other methods of integration by substitution when evaluating a definite integral it We have since learned a number of integration techniques including Substitution and Integration by Parts yet we are still unable to evaluate the above integral without resorting to a geometric interpretation This section introduces Trigonometric Substitution a method of integration that fills this gap in our integration skill
Trig Sub Chart
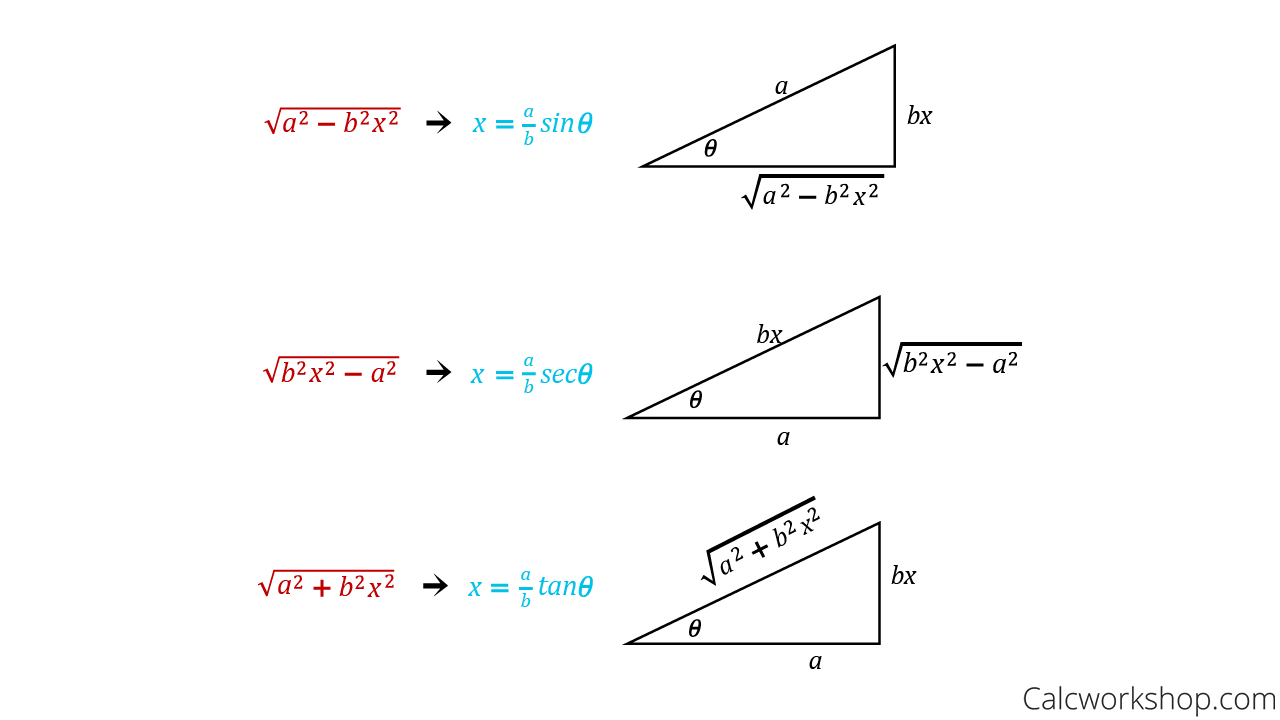
Trig Sub Chart
https://calcworkshop.com/wp-content/uploads/table-trig-substitutions.png
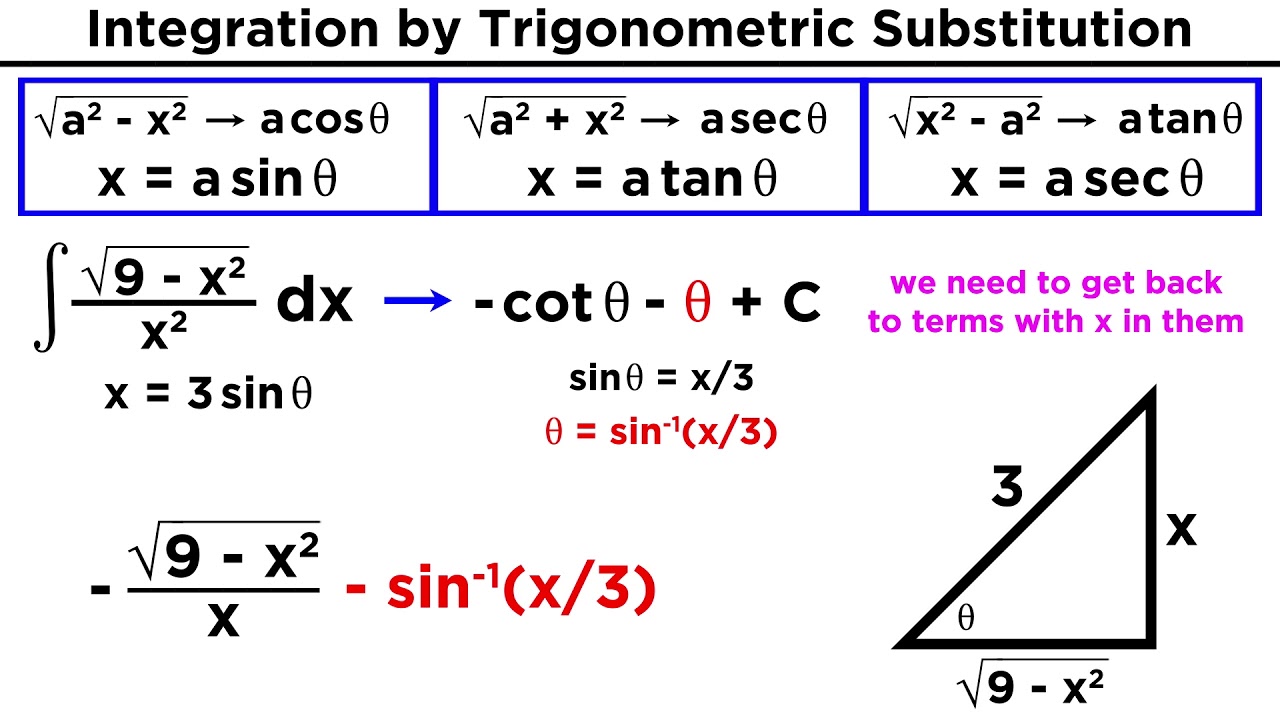
Integration By Trigonometric Substitution YouTube
https://i.ytimg.com/vi/t3rzxSgvZZk/maxresdefault.jpg

Trig Substitution Knowing All The Tri Angles Indefinite Integrals
http://schoolbag.info/mathematics/calculus/calculus.files/image659.jpg
Introduction to trigonometric substitution Substitution with x sin theta More trig sub practice Trig and u substitution together part 1 Trig and u substitution together part 2 Trig substitution with tangent More trig substitution with tangent Long trig sub problem Trigonometric substitution Math Integral Calculus Integrals In the following table we list trigonometric substitutions that are effective for the given radical expressions because of the specified trigonometric identities In each case the restric tion on is imposed to ensure that the function that defines the substitution is one to one
Trig Substitution is often used when the integrand involves a2 u2 or a2 u2 or Throughout this handout 0 a is a positive constant u2 a2 If let Logic Reduces Memorization then get Thus if integrand has try letting a sin sin a tan tan p a2 u2 p a2 u2 a2 u2 a2 u2 a sin a tan a sec u p u2 a2 19 01 28 yr mn dy The three common trigonometric substitutions are the restricted sine restricted tangent and restricted secant Thus for sine we use the domain 2 2 2 2 and for tangent we use 2 2 2 2 Depending on the convention chosen the restricted secant function is usually defined in one of two
More picture related to Trig Sub Chart

PPT 7 2 Trig Integrals PowerPoint Presentation Free Download ID
https://image1.slideserve.com/3294538/table-of-trig-substitutions-l.jpg

Trigonometric Substitution Definition Integration Examples
https://study.com/cimages/videopreview/understandingtrigsubstitution_99202.jpg

Downloadable Trig Table PDF
http://sciencenotes.org/wp-content/uploads/2015/03/TrigTable.png
Figure 7 3 7 Calculating the area of the shaded region requires evaluating an integral with a trigonometric substitution We can see that the area is A 5 3 x2 9dx To evaluate this definite integral substitute x 3sec and dx 3sec tan d We must also change the limits of integration Kind you substitute for x a certain trig function of a new variable The substitution will simplify the integrand since it will eliminate the square root Here s a table summarizing the substitution to make in each of the three kinds If use see use the sub so that and a2 x2 x asin dx acos d a2 x2 acos
Trigonometric substitution is not hard It is just a trick used to find primitives It is usually used when we have radicals within the integral sign There are three basic cases and each follow the same process The only difference between them is the trigonometric substitution we use Remember to find dx as a function of before you Every trig substitution problem reduces down to an integral involving trig functions and the majority of them will need some manipulation of the integrand in order to evaluate Show Step 5 As the final step we just need to go back to z s To do this we ll need a quick right triangle Here is that work

Trig Substitutions Cheat Sheet
https://s3.studylib.net/store/data/008718942_1-86b0de155b1feb0f6abeab28bf5525fc.png

Trigonometric Functions With Their Formulas
https://trigidentities.net/wp-content/uploads/2020/02/List-of-Trig-Functions.png
Trig Sub Chart - Trig Substitution is often used when the integrand involves a2 u2 or a2 u2 or Throughout this handout 0 a is a positive constant u2 a2 If let Logic Reduces Memorization then get Thus if integrand has try letting a sin sin a tan tan p a2 u2 p a2 u2 a2 u2 a2 u2 a sin a tan a sec u p u2 a2 19 01 28 yr mn dy