Pythagorean Theorem Notes Pdf ThePythagorean theoremis one of the most beautiful theorems in mathematics It is simple to state easy to use and highly accessible it doesn t require a huge amountofmathematical machinery to prove We llbe ableto proveit innumerous ways with what we ve learned so far
If the square of one side of a triangle is equal to the of the of the other two sides then the triangle is a triangle Decide if the following lengths can form a right triangle 14 6 8 10 15 10 24 26 16 9 12 18 17 16 30 34 Pythagorean Inequalities Theorem Figure 1 A right angled triangle with hypotenuse shown What the theorem says is that the area of the square on the hypotenuse is equal to the sum of the areas of the squares on the two shorter sides Figure 2 shows squares drawn on the hypotenuse and on the two shorter sides The theorem tells us that area A area B area C C
Pythagorean Theorem Notes Pdf

Pythagorean Theorem Notes Pdf
https://2.bp.blogspot.com/-oz4oeojF2rU/WIRG4-54ucI/AAAAAAAADJ0/NEBbUiQVLkcLA271FoKwzVzmjY0sAlDSwCEw/s1600/Pythagorean%2BTheorem%2B3.jpg

Applications Pythagorean Theorem Notes
https://s3.studylib.net/store/data/008369934_1-26a21b4ecef7b86018c46fd26f40b416-768x994.png

Notes On Understanding Pythagoras Theorem Notes LearnPick India
https://www.learnpick.in/files/noteimages/2019/cf9752263b702ca8cb483a82c3a03afd-1.jpg
Pythagoras was a Greek mathematician and philosopher who discovered one of the most famous rules in mathematics In mathematics a rule is called a theorem So the rule that Pythagoras discovered is called the Pythagorean Theorem Pythagoras c 570 B C c 490 B C 1 ACTIVITY Discovering the Pythagorean Theorem Work with a partner a Figure 1 The picture appears in The story of the greatest nations 1910 and shows Pythagoras teaching mathematics 1 2 We use here the theorem also while introducing vectors and linear spaces
The famous theorem by Pythagoras defines the relationship between the three sides of a right triangle Pythagorean Theorem says that in a right triangle the sum of the squares of the two right angle sides will always be the same as the square of the hypotenuse the long side In symbols A2 B2 C2 Pythagorean Theorem converse true too In a right triangle the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs a2 b2 c2 c is the hypotenuse IFF the triangle is a right triangle Examples Find the missing side a b c Other examples d Word Problem
More picture related to Pythagorean Theorem Notes Pdf

Free Step by step Note taking Sheets For The Pythagorean Theorem
https://i.pinimg.com/originals/e3/d9/cd/e3d9cd4e853990c190c13938b5c6635d.png

Unit 3 Pythagorean Theorem North Junior High 8th Grade Math
http://njhs8math.weebly.com/uploads/9/4/4/0/9440115/img_6324.jpg
Pythagorean Theorem Guided Notes Square Root Triangle
https://imgv2-1-f.scribdassets.com/img/document/20614972/original/2a5e9c3361/1586302596?v=1
Lecture Notes The Pythagorean Theorem page 2 b The only side here that could be the hypotenuse is the longest one measuring 13ft Therefore the two quantities we need to compare are 5ft 2 12ft 2 and 13ft 2 5ft 2 12ft 2 25ft 144ft 169ft and 13ft 2 169ft Since 169ft2 169ft2 this triangle is a right triangle with hypotenuse 13ft long c The only side here that could be the PYTHAGOREAN THEOREM In a right triangle the square of the length of the hypotenuse is equal to the sum of the squares of the length of the legs 2 2 2 hypotenuse c CONVERSE OF THE PYTHAGOREAN THEOREM If the side of a triangle has lengths a b and c such that c2 a2 b2 then the triangle is a right triangle
The Pythagorean Theorem is one of the most well known and widely used theorems in mathematics We will first look at an informal investigation of the Pythagorean Theorem and then apply this theorem to find missing sides of right triangles as well as the distance between two points Then by Pythagoras theorem x2 122 162 400 So x 20 Proof of the theorem A mathematical theorem is a logical statement If p then q where p and q are clauses involving mathematical ideas The converse of If p then q is the statement If q then p The converse may or may not be true but certainty needs a separate proof

How To Prove The Pythagorean Theorem 6 Steps with Pictures
http://www.wikihow.com/images/c/c8/Prove-the-Pythagorean-Theorem-Step-6.jpg
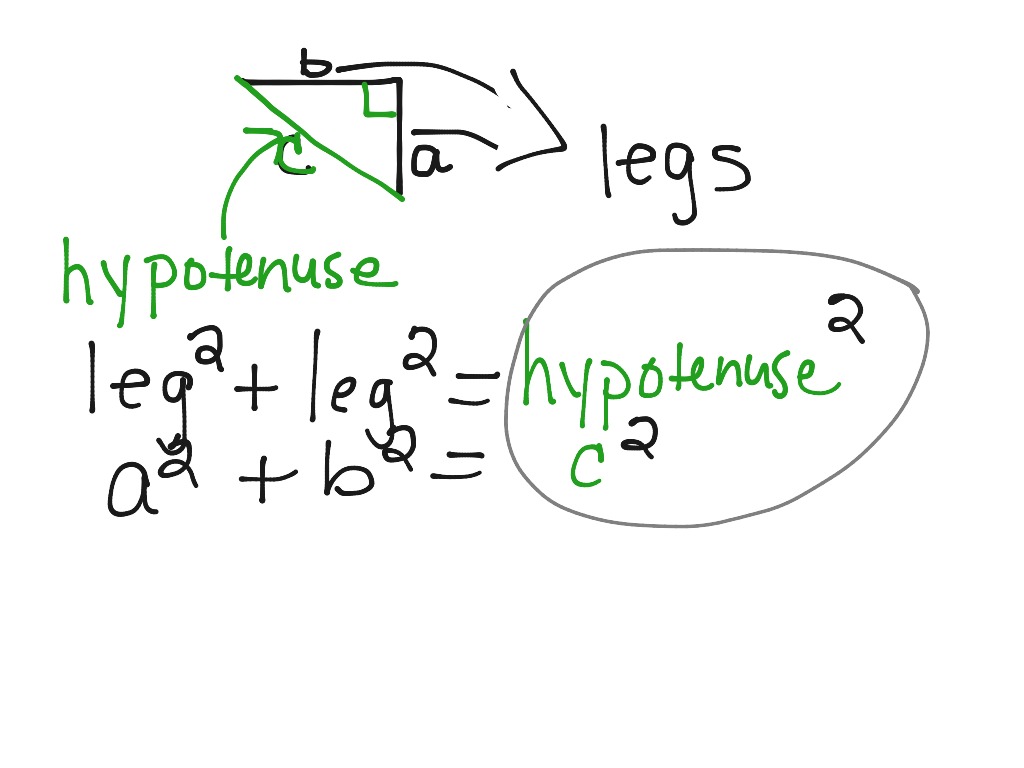
Pythagorean Theorem introduction Notes Math ShowMe
https://showme0-9071.kxcdn.com/files/1000038676/pictures/thumbs/1843247/last_thumb1420582546.jpg
Pythagorean Theorem Notes Pdf - The Pythagorean Theorem In a right triangle the sum of the squares of the lengths of the legs equals the square of the length of the hypotenuse If the three whole numbers a b and c satisfy the equation a2 b2 c2 then the numbers a b and c form a Pythagorean triple c A b ABC B a C is a right triangle so a2 b2
